向量检索基础与原理
学习目标
- 理解向量检索的核心概念和基本原理
- 了解文本嵌入和向量表示的基础知识
- 掌握向量相似度计算的主要方法
- 熟悉常见的向量索引算法和搜索技术
- 理解向量检索在AI应用中的重要作用
回顾RAG流程:
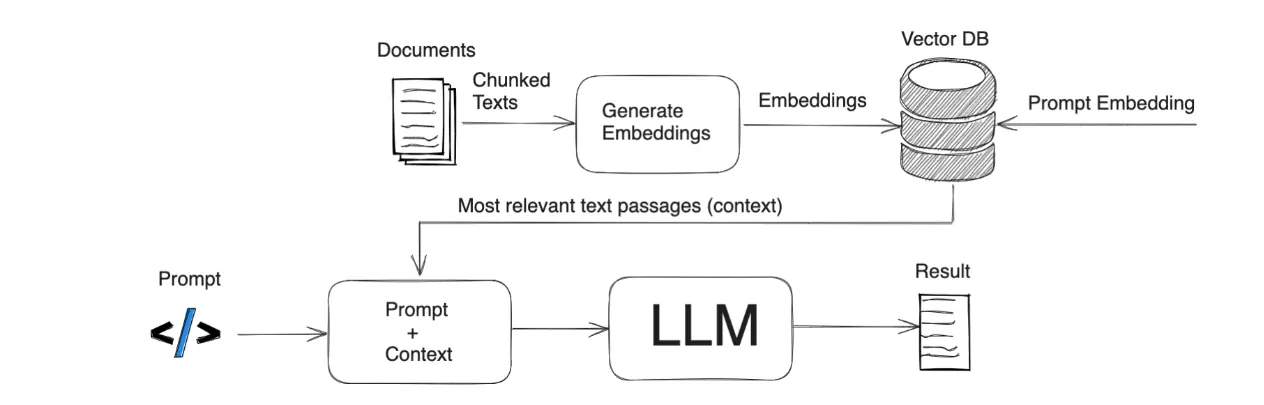
其中关键的就是Vector DB,Embedding Model。
而我们这个部分重点介绍,向量数据库及向量检索。
什么是向量检索?
向量检索(Vector Search)是一种用于在大规模向量数据集中快速寻找相似项的技术。它将传统的关键词匹配搜索扩展到了语义层面,能够理解查询的潜在含义,而不仅仅是表面的词汇匹配。
向量检索的定义:在向量空间中,寻找与给定查询向量距离最近(或相似度最高)的一组向量的过程。
多义词语义理解示例:苹果与小米
当用户搜索"苹果"或"小米"这样的词时,系统需要理解用户真正的搜索意图:
- 苹果可能指水果🍎,也可能指Apple公司或其产品📱
- 小米可能指谷物🌾,也可能指小米科技公司及其产品
传统关键词搜索只能匹配含有"苹果"或"小米"的文档,无法理解上下文语义:
搜索"苹果"→ 同时返回水果资料和电子设备信息,混杂无序
搜索"小米手环"→ 可能找不到"米环"的相关资料(词汇不完全匹配)向量检索通过语义理解解决这个问题:
# 向量表示示例
"苹果手机新款发布" → [0.2, 0.7, -0.1, ...] → 靠近电子产品语义空间
"苹果营养价值高" → [0.8, -0.3, 0.2, ...] → 靠近水果语义空间
"小米手机性价比" → [0.3, 0.6, -0.2, ...] → 靠近电子产品语义空间
"小米粥的做法" → [0.7, -0.4, 0.1, ...] → 靠近食品语义空间当用户搜索"想买新手机,苹果还是小米好?"时:
- 查询被转换为语义向量
- 系统自动识别这是关于手机的查询
- 返回苹果手机、小米手机的相关信息,而非水果或食品
甚至当用户搜索"苹果设备"时,系统能返回"iPhone"、"iPad"等相关结果,即使这些文档中没有"苹果"这个词。这展示了向量检索如何超越简单词汇匹配,提供真正的语义理解能力。
为什么需要向量检索?
在以下场景中,传统的关键词搜索往往表现不佳:
- 语义理解:用户查询"苹果手机",系统需要理解这是指设备而非水果
- 相似概念:查询"汽车"时,"轿车"、"轿跑车"等相关结果也应被检索
- 多语言搜索:用中文搜索,也能找到英文的相关内容
- 内容推荐:基于用户喜好推荐相似内容,而非简单的标签匹配
- 图像搜索:查找相似图像,而非仅依赖图像标签
向量检索通过捕捉数据的语义表示,可以很好地解决上述问题。
向量空间基础
什么是向量表示?
向量表示是将对象(如文本、图像、音频等)转换为固定维度的数值数组,以便在向量空间中进行数学运算。
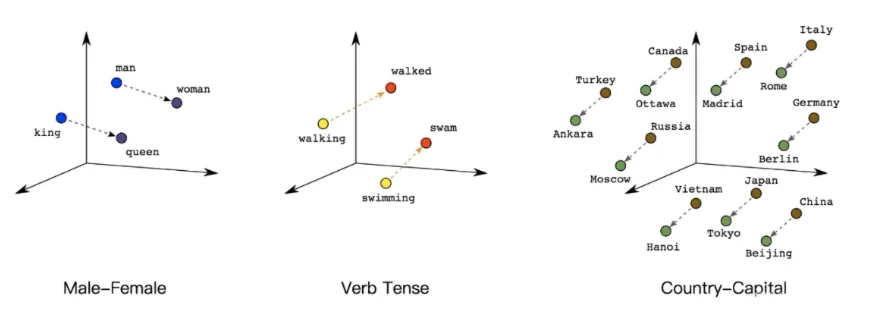
例如,一个句子可以被表示为一个300维的向量:
"人工智能正在改变世界" → [0.2, -0.5, 0.1, ..., 0.7]这个向量捕捉了句子的语义信息,使得语义相似的句子在向量空间中的位置也相近。
embedding模型(嵌入模型、特征模型、语义模型等叫法):
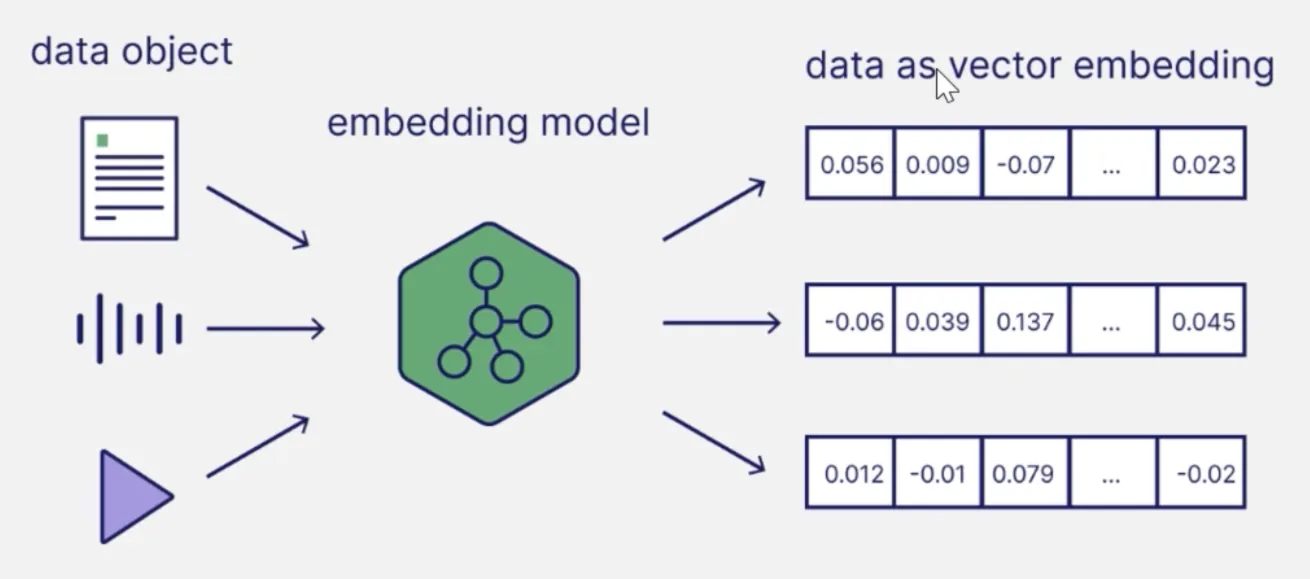
文本嵌入技术
文本嵌入(Text Embedding)是将文本转换为向量的过程,主要技术包括:
- Word2Vec:基于神经网络的词嵌入技术,学习词的分布式表示
- GloVe:结合全局矩阵分解和局部上下文窗口的词嵌入方法
- FastText:考虑子词信息的嵌入技术,适合处理形态丰富的语言
- BERT Embedding:从预训练语言模型中提取的上下文敏感嵌入
- Sentence-BERT:专为句子级嵌入优化的模型
- OpenAI Embedding:如text-embedding-ada-002等模型提供的高质量嵌入
嵌入模型示例
下面是使用不同嵌入模型的简单示例:
# 使用Sentence-BERT生成句子嵌入
from sentence_transformers import SentenceTransformer
model = SentenceTransformer('paraphrase-MiniLM-L6-v2')
sentences = [
"这是一个关于人工智能的文章",
"AI正在各个领域得到应用",
"机器学习是人工智能的一个子领域"
]
# 生成嵌入
embeddings = model.encode(sentences)
print(f"嵌入维度: {embeddings.shape}") # 例如: (3, 384)# 使用OpenAI API生成嵌入
import openai
openai.api_key = "your-api-key"
response = openai.Embedding.create(
model="text-embedding-ada-002",
input="人工智能正在改变世界"
)
embedding = response['data'][0]['embedding']
print(f"嵌入维度: {len(embedding)}") # 1536向量相似度计算
向量检索的核心是计算向量之间的相似度(或距离)。常用的度量方法包括:
1. 余弦相似度(Cosine Similarity)
定义:测量两个向量夹角的余弦值,范围[-1, 1],值越大表示越相似。
公式:
$$ \text{cos}(A, B) = \frac{\sum_{i=1}^{n} A_i B_i}{\sqrt{\sum_{i=1}^{n} A_i^2} \cdot \sqrt{\sum_{i=1}^{n} B_i^2}} $$ 特点:
- 只关注向量方向,忽略大小
- 对于文本相似度比较常用
- 计算简单,易于实现
Python实现:
import numpy as np
from scipy.spatial.distance import cosine
def cosine_similarity(vec1, vec2):
return 1 - cosine(vec1, vec2) # scipy的cosine计算的是距离,需要用1减
# 示例
vec1 = np.array([0.2, 0.5, 0.8])
vec2 = np.array([0.1, 0.4, 0.9])
similarity = cosine_similarity(vec1, vec2)
print(f"余弦相似度: {similarity}")
# 输出接近0.99
# 余弦相似度: 0.98463062942908642. 欧几里得距离(Euclidean Distance)
定义:两点在欧几里得空间中的直线距离。
公式: $$ d(A, B) = \sqrt{\sum_{i=1}^{n} (A_i - B_i)^2} $$ 特点:
- 考虑向量的绝对大小
- 适合值域相似的特征
- 距离越小表示越相似
Python实现:
from scipy.spatial.distance import euclidean
def euclidean_similarity(vec1, vec2):
# 转换为相似度,使用exp(-distance)或1/(1+distance)
distance = euclidean(vec1, vec2)
return 1 / (1 + distance)
# 示例
similarity = euclidean_similarity(vec1, vec2)
print(f"欧几里得相似度: {similarity}")
# 欧几里得相似度: 0.85236589612691993. 曼哈顿距离(Manhattan Distance)
定义:沿坐标轴方向的距离总和。
公式: $$ d(A, B) = \sum_{i=1}^{n} |A_i - B_i| $$
特点:
- 计算简单,对异常值不敏感
- 在网格状空间中有物理意义
4. 点积(Dot Product)
定义:两个向量对应元素乘积的和。
公式: $$ A \cdot B = \sum_{i=1}^{n} A_i B_i $$ 特点:
- 计算非常高效
- 对于归一化向量等价于余弦相似度
Python实现:
def dot_product(vec1, vec2):
return np.dot(vec1, vec2)相似度计算方法比较
| 度量方法 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|
| 余弦相似度 | 忽略向量大小,专注方向 | 不考虑数值差异 | 文本相似度,推荐系统 |
| 欧几里得距离 | 直观,有几何意义 | 计算量大,受维度影响 | 低维空间中的聚类 |
| 曼哈顿距离 | 计算快,对异常值不敏感 | 仅适用于网格结构 | 城市街区类问题 |
| 点积 | 计算极其高效 | 值域不固定 | 归一化向量的相似度 |
在实际应用中,余弦相似度和点积(对归一化向量)是向量检索中最常用的相似度度量方法。
向量索引技术
当向量数量达到百万或更多时,暴力搜索(与每个向量计算相似度)变得不可行。向量索引技术通过构建特殊的数据结构,实现近似最近邻(ANN: Approximate Nearest Neighbor)搜索,大幅提高检索效率。
主要的向量索引算法
1. 树形结构
KD-Tree(K-Dimensional Tree):
- 原理:将空间递归划分为子空间
- 优点:对低维数据效果好
- 缺点:高维数据(>20维)性能急剧下降
Ball Tree:
- 原理:基于超球体划分空间
- 优点:在高维空间中比KD-Tree更有效
- 缺点:构建成本高
2. 量化方法
PQ(Product Quantization):
- 原理:将高维向量分解为低维子向量,然后量化
- 优点:内存占用小,查询速度快
- 缺点:精度有损失
SQ(Scalar Quantization):
- 原理:对向量每个维度进行量化
- 优点:实现简单
- 缺点:精度损失较大
3. 基于图的方法
HNSW(Hierarchical Navigable Small World):
- 原理:多层图结构,上层为下层的快速索引
- 优点:检索速度极快,精度高
- 缺点:内存占用大,不支持动态删除
NSG(Navigating Spreading-out Graph):
- 原理:优化的图结构,减少冗余边
- 优点:比HNSW内存效率更高
- 缺点:构建复杂
4. 基于哈希的方法
LSH(Locality-Sensitive Hashing):
- 原理:相似向量映射到相同的桶
- 优点:内存效率高,适合超大规模数据
- 缺点:召回率较低
向量索引库比较
| 索引库 | 算法 | 特点 | 适用场景 |
|---|---|---|---|
| Faiss | PQ, HNSW, IVF等 | 高性能,适合GPU加速 | 大规模、高维向量 |
| Annoy | 随机投影树 | 构建快,内存占用小 | 静态数据集 |
| NMSLIB | HNSW, SW-graph | 查询速度最快 | 需要高性能检索 |
| ScaNN | AH, ANNS | Google开发,高精度 | 大规模推荐系统 |
| Milvus | 多种算法 | 分布式,易扩展 | 企业级向量数据库 |
实践: HNSW算法示例
HNSW (Hierarchical Navigable Small World) 是当前最流行的向量索引算法之一,以下是使用它的简单示例:
import numpy as np
import hnswlib
# 生成示例数据
dim = 128 # 向量维度
num_elements = 10000 # 向量数量
# 随机生成向量
data = np.random.random((num_elements, dim)).astype('float32')
# 初始化HNSW索引
index = hnswlib.Index(space='cosine', dim=dim) # 可选space: cosine, l2, ip
index.init_index(max_elements=num_elements, ef_construction=200, M=16)
# 添加向量到索引
index.add_items(data)
# 设置搜索参数
index.set_ef(50) # ef越大,搜索越精确但越慢
# 执行搜索
query_vector = np.random.random(dim).astype('float32')
labels, distances = index.knn_query(query_vector, k=5)
print("最相似的5个向量索引:", labels)
print("对应的相似度:", 1 - np.array(distances)) # 对于cosine space,转换为相似度
# 保存和加载索引
index.save_index("hnsw_index.bin")
loaded_index = hnswlib.Index(space='cosine', dim=dim)
loaded_index.load_index("hnsw_index.bin", max_elements=num_elements)向量检索与大语言模型
向量检索在大语言模型(LLM)应用中扮演着至关重要的角色,特别是在克服LLM的以下限制方面:
- 知识更新:LLM知识在预训练时固定,向量检索可实时补充最新信息
- 上下文窗口限制:通过检索最相关内容,最大化利用有限的上下文窗口
- 幻觉问题:检索到的事实内容可降低模型生成虚假信息的概率
- 领域专业性:检索行业专业文档,增强模型在特定领域的表现
典型应用:RAG架构
RAG(Retrieval-Augmented Generation)是结合向量检索和生成模型的经典架构,工作流程如下:
索引阶段:
- 将知识库文档分块(chunking)
- 使用嵌入模型为每个块生成向量表示
- 将向量存入向量数据库
查询阶段:
- 将用户问题转换为查询向量
- 在向量数据库中检索最相关的文档块
- 将检索到的内容与原始问题一起发送给LLM
- LLM基于检索内容生成回答
# RAG简化实现示例
from sentence_transformers import SentenceTransformer
import numpy as np
import requests
import json
# 1. 准备向量模型
model = SentenceTransformer('paraphrase-MiniLM-L6-v2')
# 2. 示例知识库
documents = [
"Python是一种高级编程语言,以易读性和简洁性著称。",
"深度学习是机器学习的一个分支,使用多层神经网络进行学习。",
"向量数据库专门设计用于存储和查询高维向量数据。",
"大语言模型如GPT和DeepSeek具有强大的自然语言理解能力。"
]
# 3. 生成文档向量
doc_embeddings = model.encode(documents)
# 4. 简单的向量检索函数
def retrieve(query, top_k=2):
# 编码查询
query_embedding = model.encode([query])[0]
# 计算相似度
similarities = [np.dot(query_embedding, doc_embedding)
for doc_embedding in doc_embeddings]
# 找出最相似的文档
top_indices = np.argsort(similarities)[-top_k:][::-1]
return [documents[i] for i in top_indices]
# 5. 简化的LLM接口
def generate_answer(query, context):
# 这里使用DeepSeek API (简化示例)
prompt = f"""根据以下上下文回答问题。如果上下文中没有相关信息,请说"我不知道"。
上下文:
{' '.join(context)}
问题: {query}
回答:"""
# 实际应用中,这里应该调用DeepSeek API
print(f"发送到LLM的提示:\n{prompt}")
# 模拟LLM返回
return "这是基于检索内容的LLM生成回答。"
# 6. RAG流程
def rag(query):
# 检索相关文档
relevant_docs = retrieve(query)
print(f"检索到的文档: {relevant_docs}")
# 生成回答
answer = generate_answer(query, relevant_docs)
return answer
# 测试
query = "什么是大语言模型?"
answer = rag(query)
print(f"回答: {answer}")小结
在本节中,我们学习了:
- 向量检索的基本概念和重要性
- 文本嵌入技术和向量表示基础
- 常用的向量相似度计算方法
- 主流向量索引算法及其特点
- 向量检索在大语言模型应用中的关键作用
向量检索是现代AI应用的基础设施,尤其在大语言模型应用中扮演着至关重要的角色。在接下来的章节中,我们将深入学习向量数据库的应用实践,以及如何构建高效的检索系统。
思考题
- 为什么余弦相似度在向量检索中比欧几里得距离更常用?
- HNSW算法相比传统树形结构算法有哪些优势?
- 在RAG架构中,文档分块(chunking)的大小和方式会如何影响最终的检索效果?
- 如何选择合适的嵌入模型来表示特定领域的文本内容?